07 February 2019
Proper Coloring of a Graph
Program carried out in the academic field. It is one of my best works and of which I’m most proud.
What is a graph?
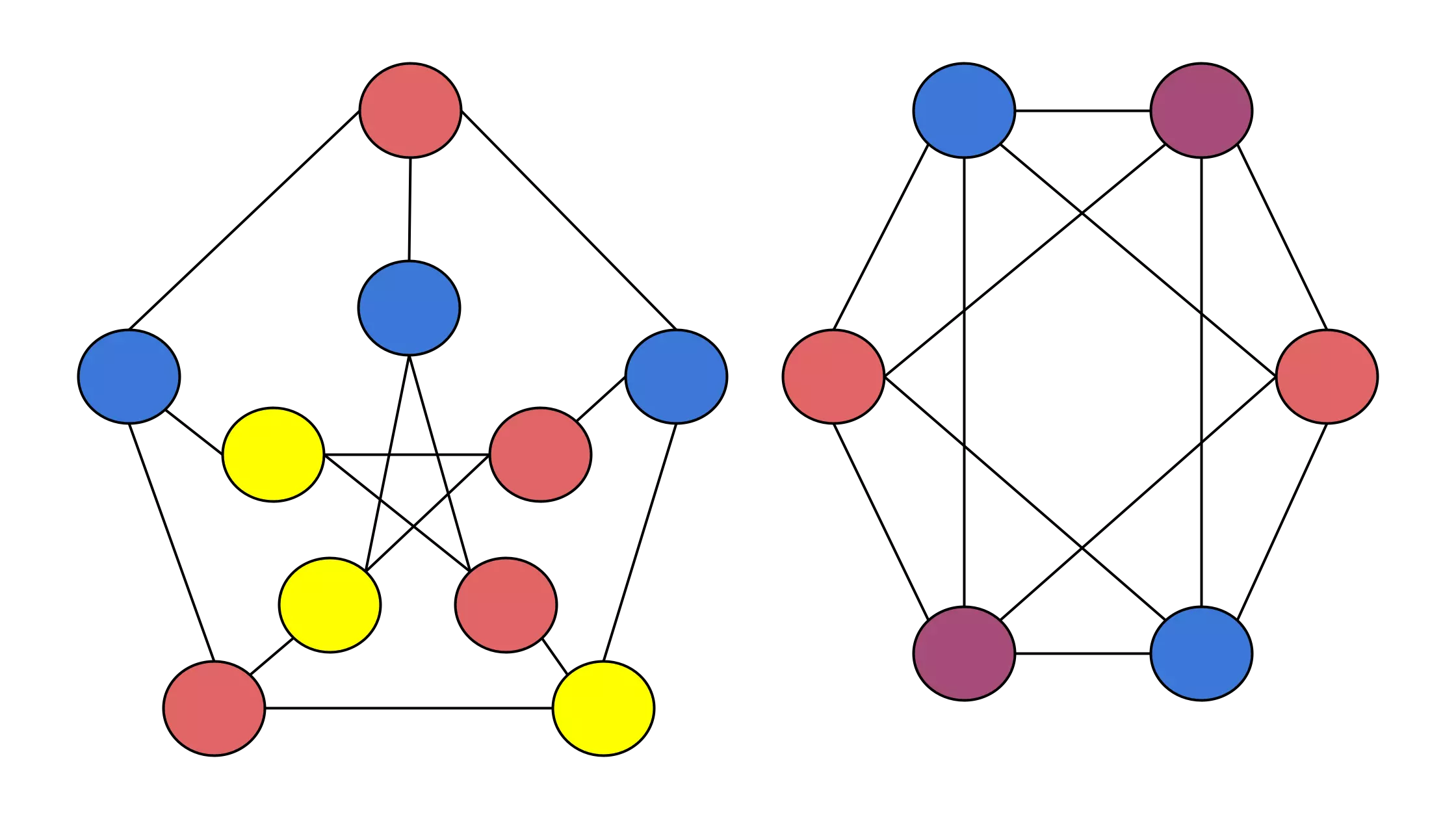
A graph is a set of vertices intercommunicated by edges (as in the cover image). They are useful for represent certain types of problems, ej: Travelling salesman problem.
What is a graph colored?
Each vertex is assigned a color, with the condition that there are not 2 or more vertex that are connected by any edge and have the same color.
A trivial coloring for a graph would be to assign a different color to each vertex.
What is a proper coloring graph?
A proper coloring graph, is a coloring of a graph, with the added condition that use the minor numbers of colors possible.
We will call χ (Chi) the minimum number of colors necessary to generate a proper coloring of the graph.
It turns out that, except for particular cases, there is no (fast) polynomial algorithm to generate a proper coloring of a Graph. Because of this we are going to use a heuristic, that is, a function that approximates the value of χ. This function will be to use Greedy algorithm multiple times, which depends on the initial ordering of the vertices.
This program was designed from the beginning to handle larges graphs, of the order of millions of vertices and tens of millions of edges, and use Greedy a thousand times! Therefore, to support such magnitudes, it was necessary to constantly think about efficiency throughout the development process.
If you are not very careful you could develop a program that takes days or even months to finish!
For more specific information and how to use it, see the source code here.